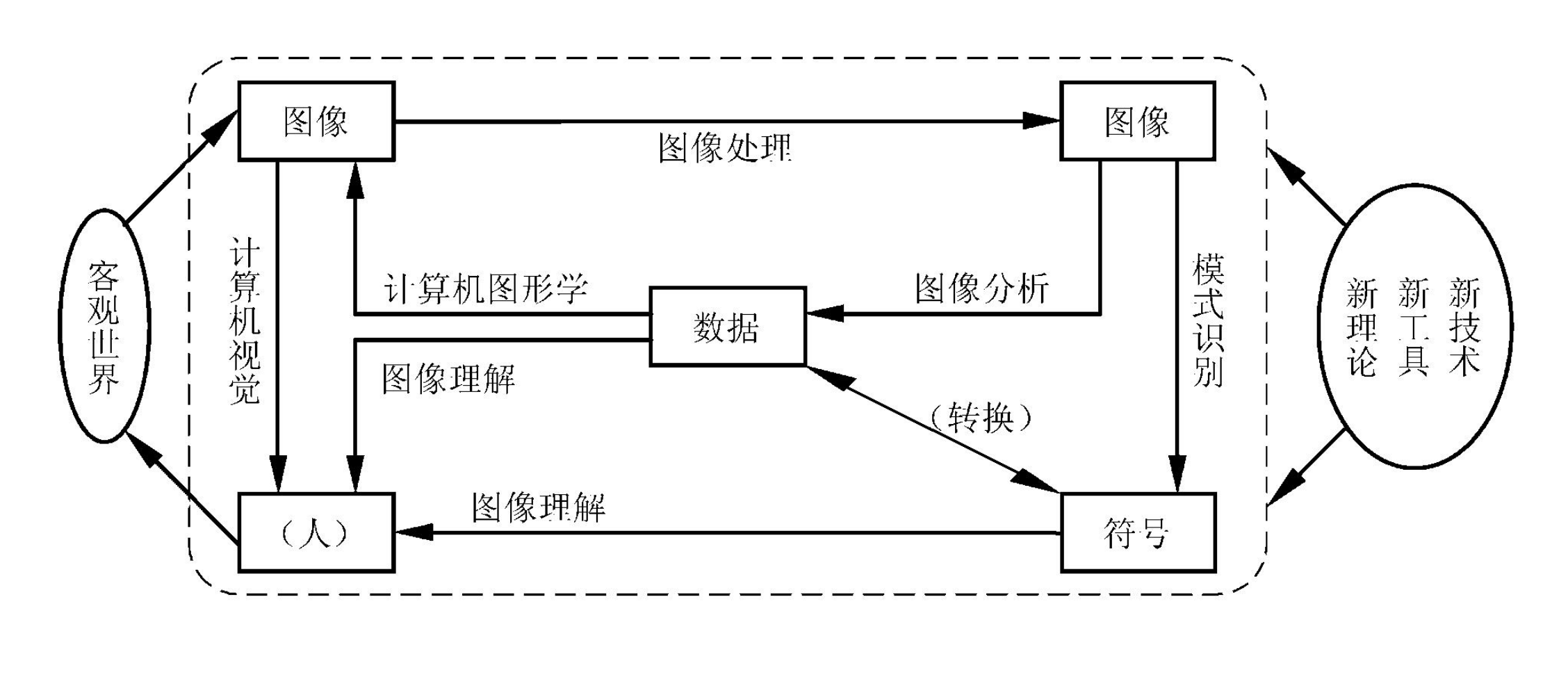
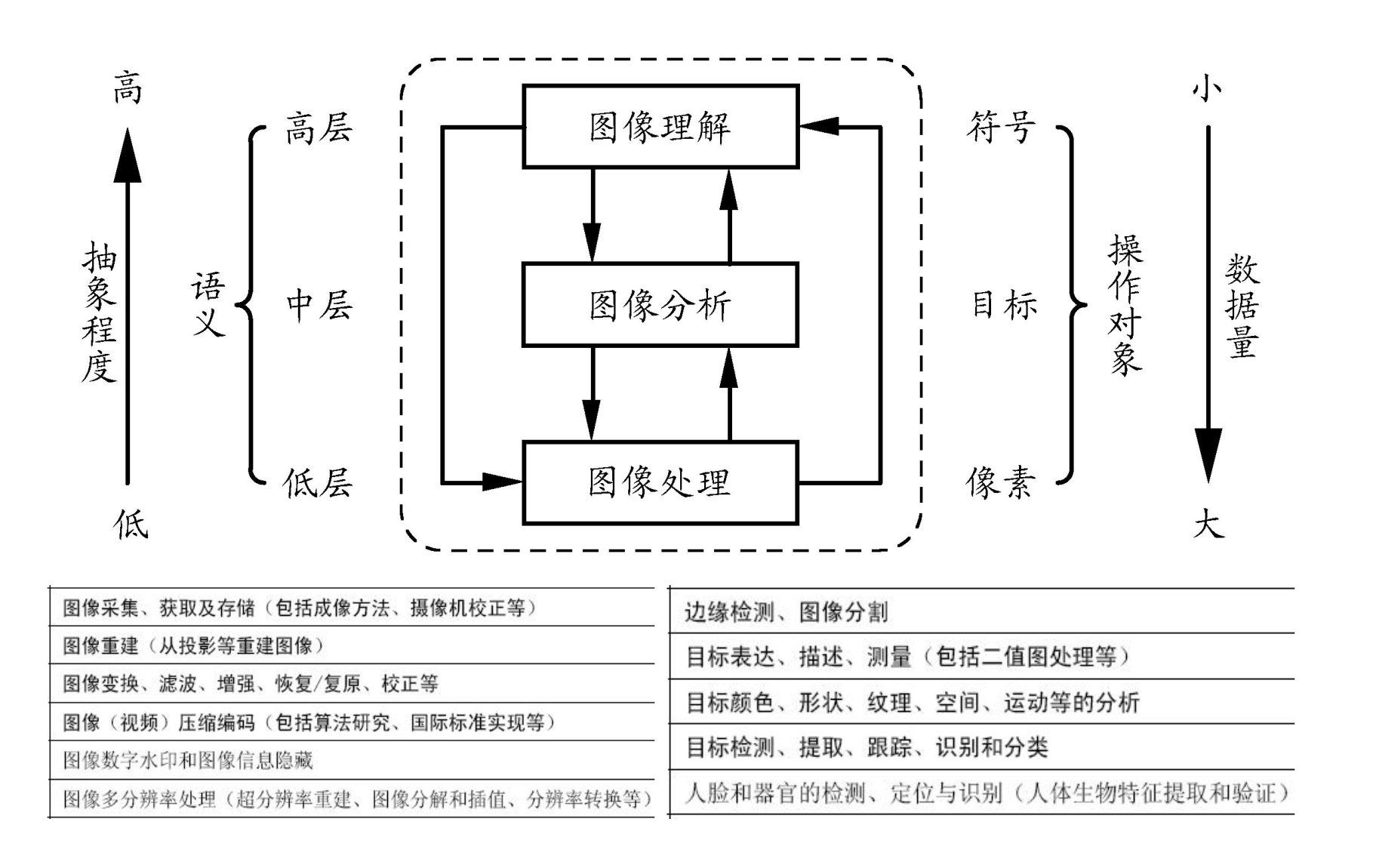
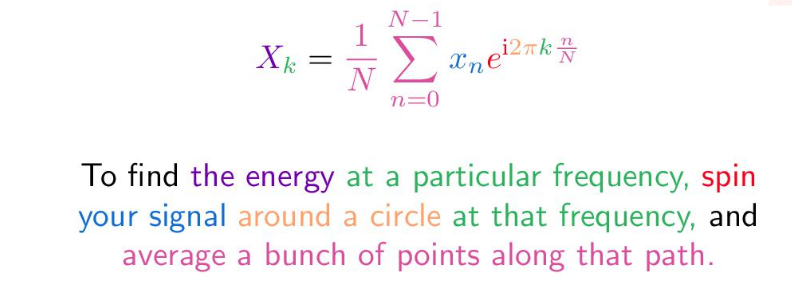传统视觉理论及实践

什么是计算机视觉

计算机视觉（Computer Vision）是一门研究如何使机器“看”的科学，它利用摄像头和计算机算法，让机器能够像人一样“看”，并且能够从中获取信息。计算机视觉是一门多领域交叉的学科，涉及到计算机科学、数学、物理学、生物学、心理学等多个学科。

计算机视觉的研究对象是图像，目的是从图像中获取信息。

Q: 从图像中能获取什么信息？
A: 物体的位置、大小、形状、颜色、纹理、运动等。

图像

图像的类型


彩色图像	多光谱图像	纹理图像
立体图像	深度图像	3D图像
序列图像	投影重建图像	合成图像

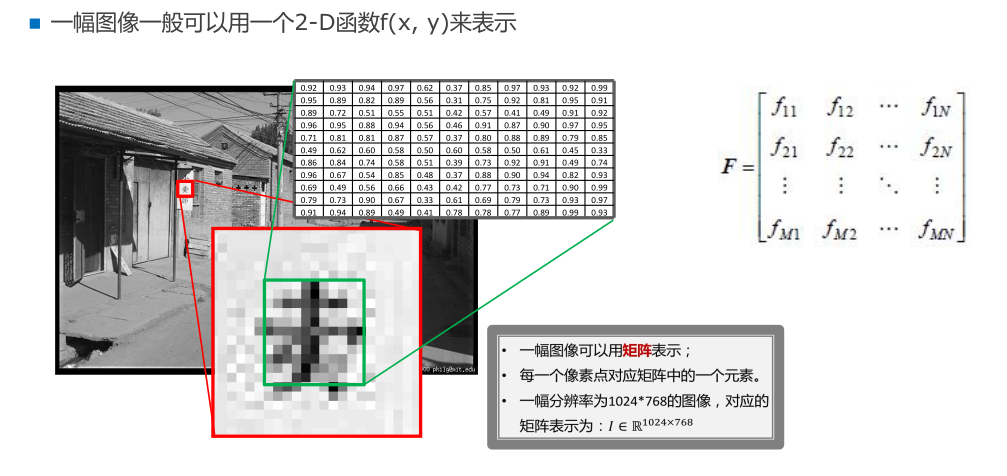
图像的存储方式

图像由像素组成，像素是组成图像的最小单元，每个像素可以看做一个多维向量。

例如，一幅的灰度图像可以看做一个的矩阵，其中每个元素表示一个像素的灰度值；
一幅的彩色图像可以看做一个的张量，其中每个元素表示一个像素的 RGB 三个通道的值。

我们可以把彩色图像看做是三个灰度图像的叠加，每个灰度图像对应一个通道，一般是红、绿、蓝三个通道。

Q: 为什么是红、绿、蓝三个通道？
A: 人眼就是由红、绿、蓝三种颜色的感光细胞感觉光线的。

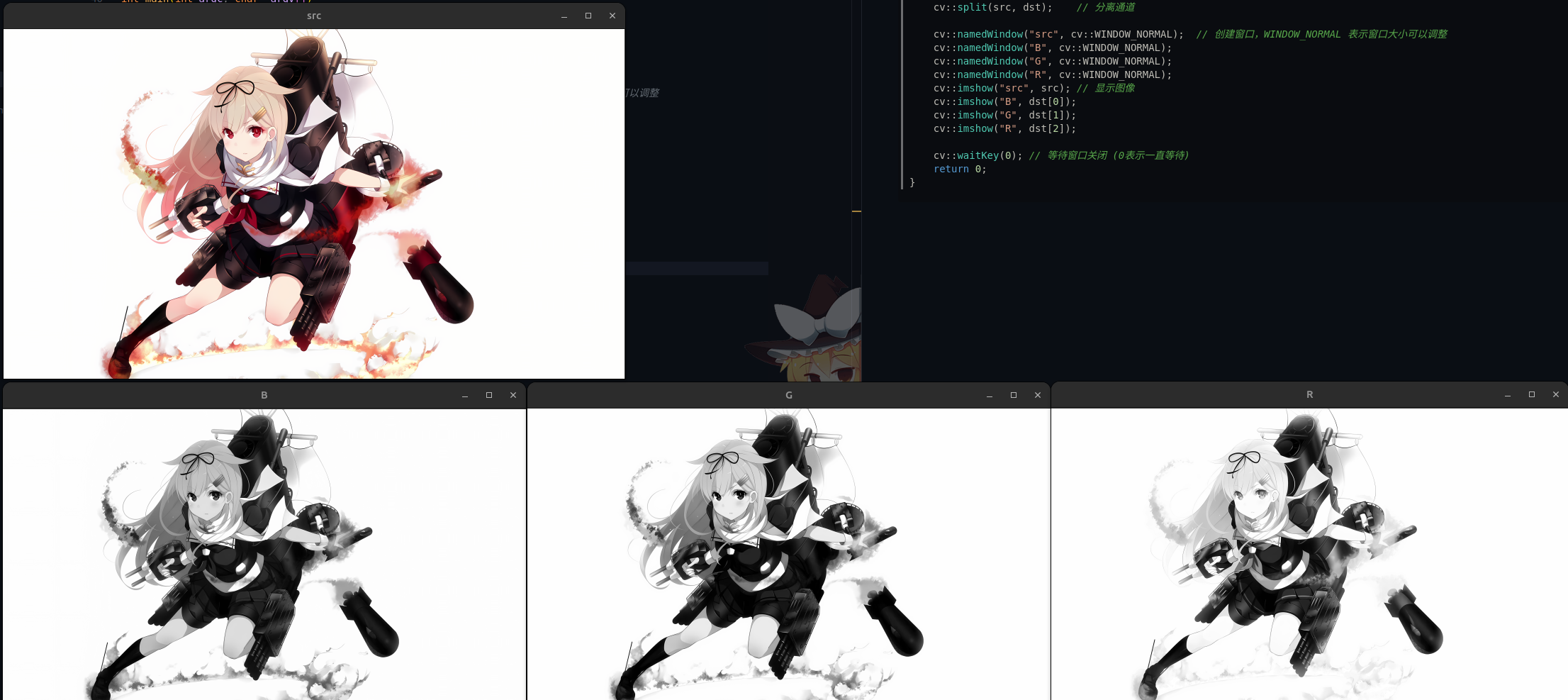
例：分离 RGB 通道（opencv, cpp）。

#include <opencv2/opencv.hpp>

#include <vector>

int main(int argc, char* argv[])
{
    cv::Mat src = cv::imread(argv[1]);  // 读取图像
    std::vector<cv::Mat> dst;   // 存储分离后的通道

    cv::split(src, dst);    // 分离通道

    cv::namedWindow("src", cv::WINDOW_NORMAL);  // 创建窗口，WINDOW_NORMAL 表示窗口大小可以调整
    cv::namedWindow("B", cv::WINDOW_NORMAL);
    cv::namedWindow("G", cv::WINDOW_NORMAL);
    cv::namedWindow("R", cv::WINDOW_NORMAL);
    cv::imshow("src", src); // 显示图像
    cv::imshow("B", dst[0]);
    cv::imshow("G", dst[1]);
    cv::imshow("R", dst[2]);
    
    cv::waitKey(0); // 等待窗口关闭 (0表示一直等待)
    return 0;
}

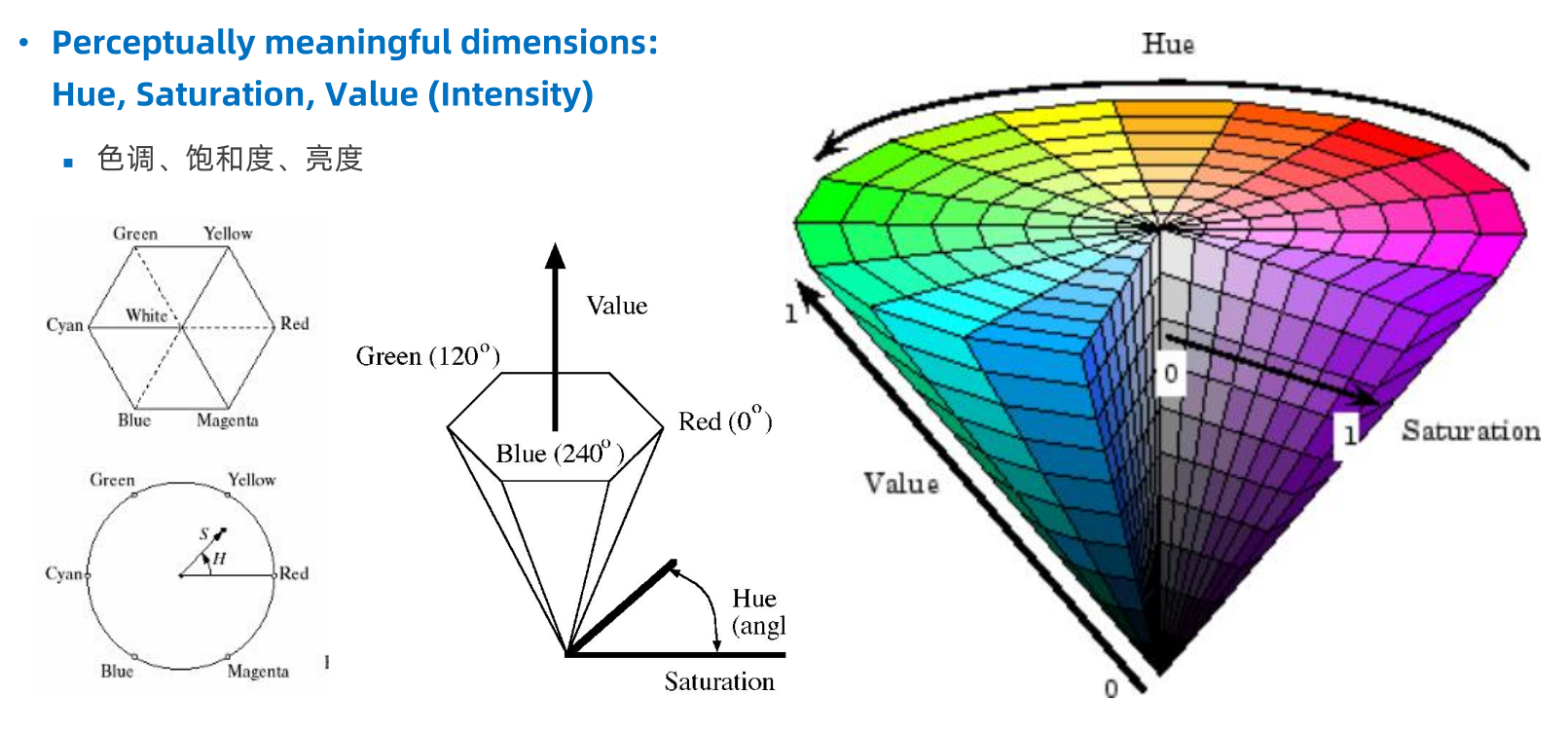
色彩空间

上面提到了 RGB 色彩空间，除了 RGB 色彩空间，还有很多其他的色彩空间，例如 CMY、HSI、HSV 等。不同的色彩空间有不同的特点，适用于不同的场景。

例：RGB 转 HSV 并分离三通道。

#include <opencv2/opencv.hpp>

#include <vector>

int main(int argc, char* argv[])
{
    cv::Mat src = cv::imread(argv[1]);  // 读取图像
    cv::Mat hsv;    // 存储 HSV 图像
    std::vector<cv::Mat> dst;   // 存储分离后的通道

    cv::cvtColor(src, hsv, cv::COLOR_BGR2HSV);    // RGB 转 HSV
    cv::split(hsv, dst);    // 分离通道

    cv::namedWindow("src", cv::WINDOW_NORMAL);  // 创建窗口，WINDOW_NORMAL 表示窗口大小可以调整
    cv::namedWindow("H", cv::WINDOW_NORMAL);
    cv::namedWindow("S", cv::WINDOW_NORMAL);
    cv::namedWindow("V", cv::WINDOW_NORMAL);
    cv::imshow("src", src); // 显示图像
    cv::imshow("H", dst[0]);
    cv::imshow("S", dst[1]);
    cv::imshow("V", dst[2]);
    
    cv::waitKey(0); // 等待窗口关闭 (0表示一直等待)
    return 0;
}

Q: HSV 相较于 RGB 有什么优势？
A: HSV 色彩空间更符合人类视觉感知，更容易区分颜色。

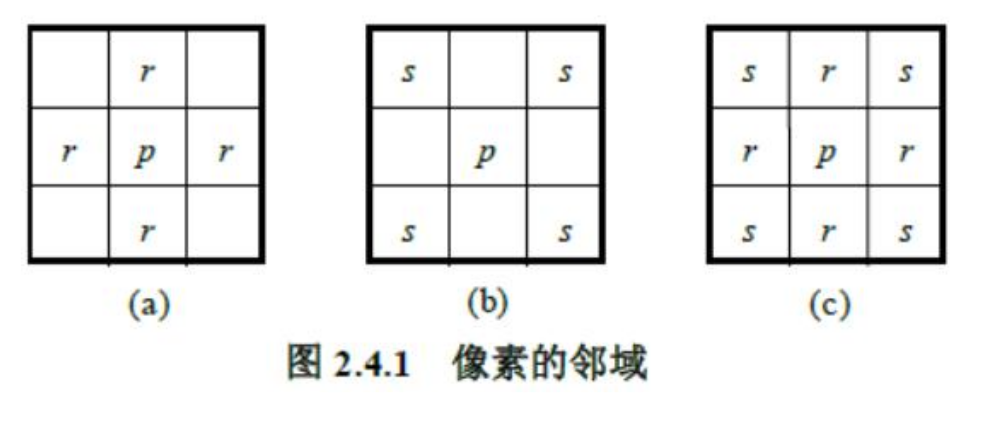
补充：像素的基本操作

邻域

四邻域：上下左右四个像素
对角邻域：左上、右上、左下、右下四个像素
八邻域：四邻域 + 对角邻域

像素的距离

欧式距离：
曼哈顿距离：
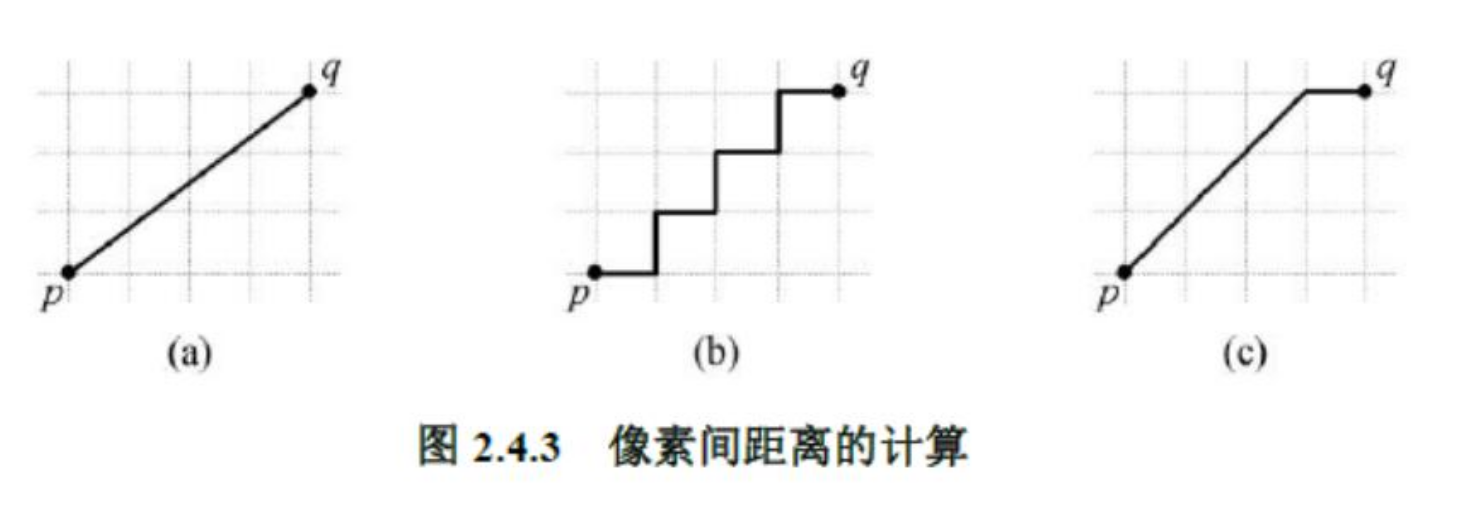
切比雪夫距离(棋盘距离)：

滤波

图像滤波是图像处理中的一种基本操作，它可以使图像变得更加平滑，去除噪声，增强图像的细节等。

卷积

卷积是图像滤波的基础，它是一种数学运算，用于图像处理中的滤波操作。

其数学表达式为：

其中，是原始图像，是卷积核，是卷积后的图像，是卷积核的半径，是图像坐标，是卷积核坐标。

例如，下面是一个的卷积核：

例：使用卷积处理图像。

#include <opencv2/opencv.hpp>

int main(int argc, char* argv[]) {
    cv::Mat src = cv::imread(argv[1]);
    cv::Mat dst;
    cv::Mat kernel; // 卷积核

    kernel = (cv::Mat_<float>(3, 3) << 0, -1, 0, -1, 4, -1, 0, -1, 0);  // 创建卷积核

    cv::filter2D(src, dst, -1, kernel); // 卷积
    
    cv::namedWindow("src", cv::WINDOW_NORMAL);
    cv::namedWindow("dst", cv::WINDOW_NORMAL);
    cv::imshow("src", src);
    cv::imshow("dst", dst);
    
    cv::waitKey(0);
    return 0;
}

常见滤波器

均值滤波

均值滤波是一种最简单的滤波器，它将每个像素的值替换为其邻域像素的平均值。

中值滤波

中值滤波是一种非线性滤波器，它将每个像素的值替换为其邻域像素的中值。

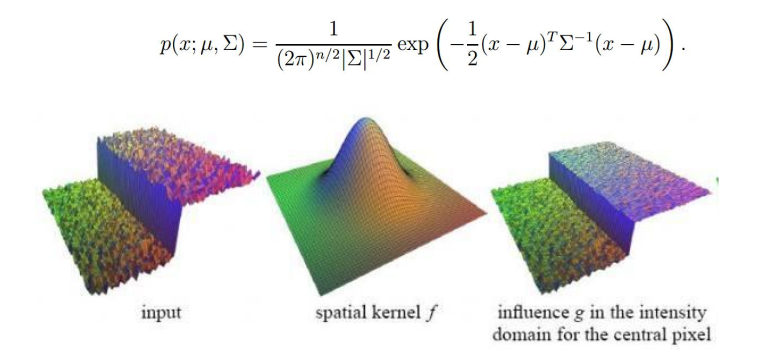
高斯滤波

高斯滤波是一种线性滤波器，它将每个像素的值替换为其邻域像素的加权平均值。

先按照公式计算权重，然后归一化到和为1。

如：

锐化滤波

锐化滤波是一种增强图像细节的滤波器，它强调与局部平均之间的差异。

当然，卷积核不一定是的，也可以是其他尺寸的。如下图所示，是一个的高斯卷积核：

补充：频域

傅里叶变换是一种信号处理中常用的方法，它可以将信号从时域转换到频域，从而更好地理解信号的特征。

将图像看做是一个二维信号，我们可以对图像进行傅里叶变换，得到图像的频谱：

例如：

FFT的结果是复数形式，保留了图像的全部信息，但去绝对值得到的频谱图只表现了振幅而没有体现相位。

在频域中，我们可以对图像进行滤波，然后再进行逆变换，得到滤波后的图像。

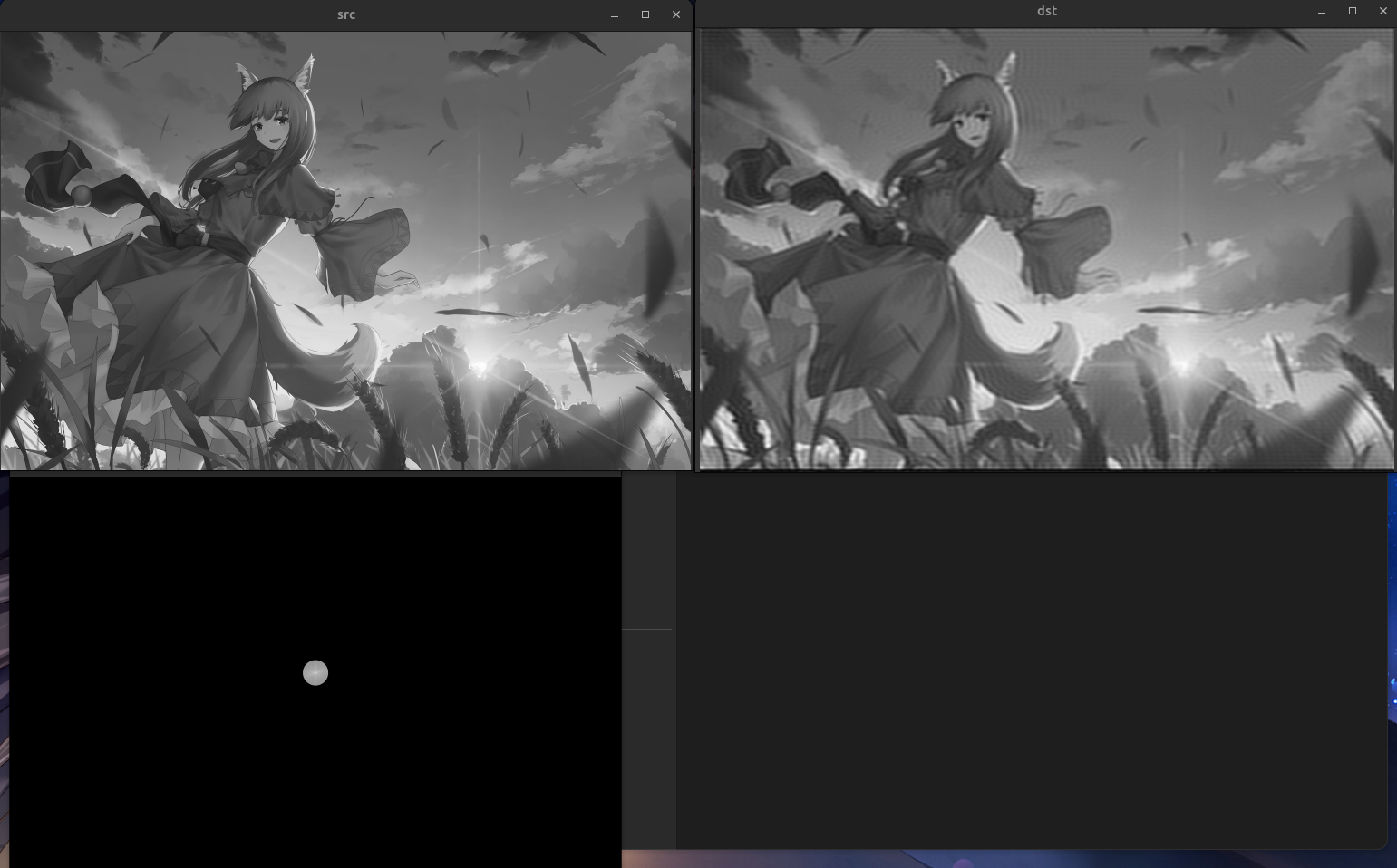
例：使用 DFT 进行频域低通滤波。

#include <opencv2/opencv.hpp>

int main(int argc, char* argv[]) {
    cv::Mat src = cv::imread(argv[1]);
    cv::Mat dst;
    cv::Mat padded; // 填充后的图像
    cv::Mat complexI; // 复数形式的频谱图

    cv::cvtColor(src, src, cv::COLOR_BGR2GRAY); // 转换为灰度图
    src.convertTo(padded, CV_32F); // 转换为浮点型
    int m = cv::getOptimalDFTSize(padded.rows);
    int n = cv::getOptimalDFTSize(padded.cols);

    cv::copyMakeBorder(padded, padded, 0, m - padded.rows, 0, n - padded.cols, cv::BORDER_CONSTANT, cv::Scalar::all(0)); // 填充图像

    cv::dft(padded, complexI, cv::DFT_COMPLEX_OUTPUT); // 傅里叶变换
    // 分成四个象限
    cv::Mat q0 = complexI(cv::Rect(0, 0, complexI.cols / 2, complexI.rows / 2));
    cv::Mat q1 = complexI(cv::Rect(complexI.cols / 2, 0, complexI.cols / 2, complexI.rows / 2));
    cv::Mat q2 = complexI(cv::Rect(0, complexI.rows / 2, complexI.cols / 2, complexI.rows / 2));
    cv::Mat q3 = complexI(cv::Rect(complexI.cols / 2, complexI.rows / 2, complexI.cols / 2, complexI.rows / 2));
    // 交换象限
    cv::Mat tmp;
    q0.copyTo(tmp);
    q3.copyTo(q0);
    tmp.copyTo(q3);
    q1.copyTo(tmp);
    q2.copyTo(q1);
    tmp.copyTo(q2);
    
    // 生成低通滤波器
    int radius = 100;
    cv::Mat lowPass = cv::Mat::zeros(complexI.size(), CV_32FC2);
    cv::Point center = cv::Point(lowPass.cols / 2, lowPass.rows / 2);
    cv::circle(lowPass, center, radius, cv::Scalar(1), -1);

    // 滤波
    cv::mulSpectrums(complexI, lowPass, complexI, 0);

    cv::namedWindow("complexI", cv::WINDOW_NORMAL);
    cv::Mat plane[] = { cv::Mat::zeros(complexI.size(), CV_32F),
                        cv::Mat::zeros(complexI.size(), CV_32F) };
    cv::split(complexI, plane);
    cv::magnitude(plane[0], plane[1], plane[0]);    // 求幅值
    cv::log(plane[0] + cv::Scalar::all(1), plane[0]);   // 对数变换，方便显示
    cv::normalize(plane[0], plane[0], 0, 1, cv::NORM_MINMAX);   // 归一化
    cv::imshow("complexI", plane[0]);   // 显示频谱图

    // 交换象限
    q0.copyTo(tmp);
    q3.copyTo(q0);
    tmp.copyTo(q3);
    q1.copyTo(tmp);
    q2.copyTo(q1);
    tmp.copyTo(q2);

    cv::idft(complexI, dst, cv::DFT_SCALE | cv::DFT_REAL_OUTPUT); // 傅里叶逆变换

    cv::normalize(dst, dst, 0, 255, cv::NORM_MINMAX); // 归一化
    dst.convertTo(dst, CV_8UC1); // 转换为8位图

    cv::namedWindow("src", cv::WINDOW_NORMAL);
    cv::namedWindow("dst", cv::WINDOW_NORMAL);
    cv::imshow("src", src);
    cv::imshow("dst", dst);

    cv::waitKey(0);
    return 0;
}

Q: 高通滤波？
A: 高通滤波后，图像的低频部分会被去除，只保留高频部分，使图像的边界更突出。

边缘检测

边缘检测是图像处理中的一种基本操作，它可以检测图像中的边缘，从而提取出图像的轮廓。

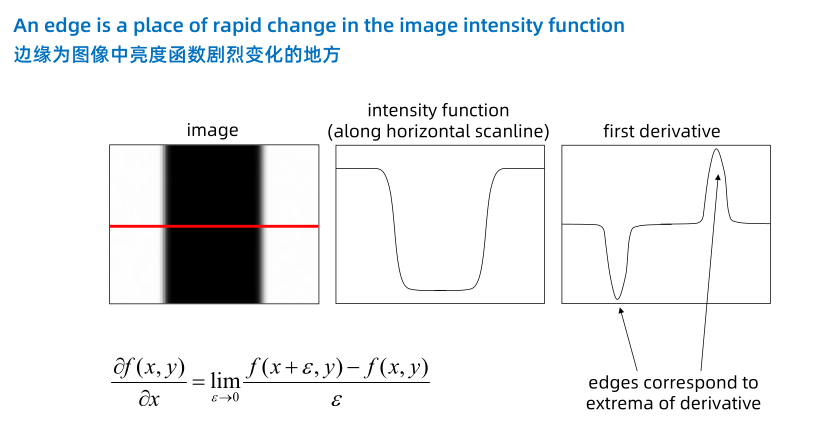
卷积微分

图像中的边缘可以看做是图像灰度的突变，因此我们可以通过对图像进行微分来检测边缘。

下面给出二维图像的偏导：

上述公式推导过程简单，这里不再赘述。由此，我们可以得到一维卷积核：

直接对图像求导会受到噪声的干扰，因此一般需要对图像先做一次平滑，减少噪声的干扰，再做求导。

Sobel 算子

Sobel 算子是一种常用的边缘检测算子，它是一种线性滤波器，可以检测图像中的水平和垂直边缘。

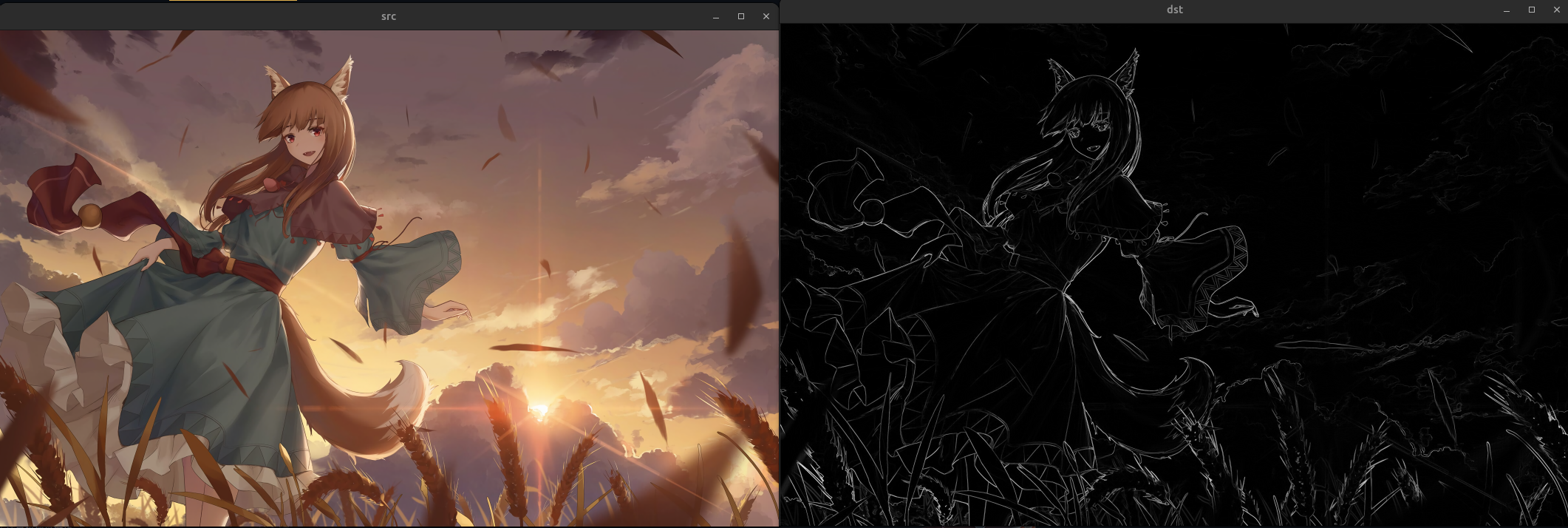
例：使用 Sobel 算子进行边缘检测。

#include <opencv2/opencv.hpp>

int main(int argc, char* argv[]) {
    cv::Mat src = cv::imread(argv[1]);
    cv::Mat dst;
    cv::Mat gray;
    cv::Mat grad_x, grad_y;
    cv::Mat abs_grad_x, abs_grad_y;

    cv::cvtColor(src, gray, cv::COLOR_BGR2GRAY); // 转换为灰度图
    cv::Sobel(gray, grad_x, CV_16S, 1, 0, 3); // x 方向梯度
    cv::Sobel(gray, grad_y, CV_16S, 0, 1, 3); // y 方向梯度
    cv::convertScaleAbs(grad_x, abs_grad_x); // 转换为8位图
    cv::convertScaleAbs(grad_y, abs_grad_y); // 转换为8位图
    cv::addWeighted(abs_grad_x, 0.5, abs_grad_y, 0.5, 0, dst); // 合并梯度

    cv::namedWindow("src", cv::WINDOW_NORMAL);
    cv::namedWindow("dst", cv::WINDOW_NORMAL);
    cv::imshow("src", src);
    cv::imshow("dst", dst);

    cv::waitKey(0);
    return 0;
}

sobel 算子是一种有限差分算子，相同的有限差分算子还有 Prewitt、Roberts、Scharr 等。

Prewitt

Roberts

Scharr

不仅有水平和垂直方向的，还有对角方向的。

拉普拉斯算子

拉普拉斯算子是一种二阶微分算子，可以检测图像中的边缘。

其数学表达式为：

由上式我们可以得到拉普拉斯算子的卷积核：

DoG & LoG

DoG（Difference of Gaussian）是高斯滤波的差分，指的是先对图像进行两次高斯滤波，然后再求差分。

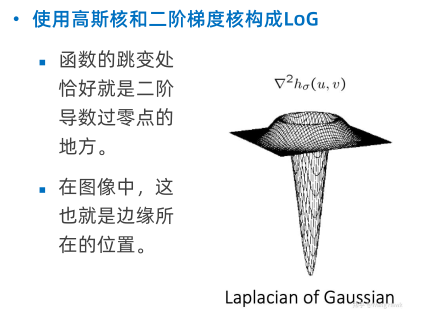
LoG（Laplacian of Gaussian）是高斯滤波的拉普拉斯，指的是先对图像进行高斯滤波，然后再求拉普拉斯。

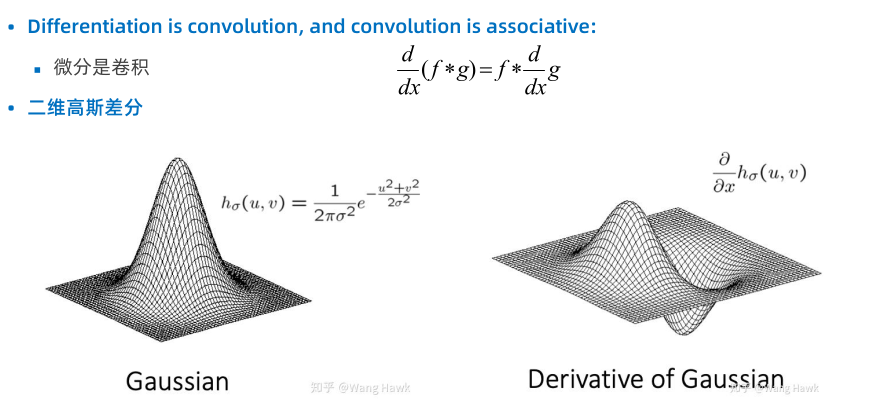
卷积的微分定理

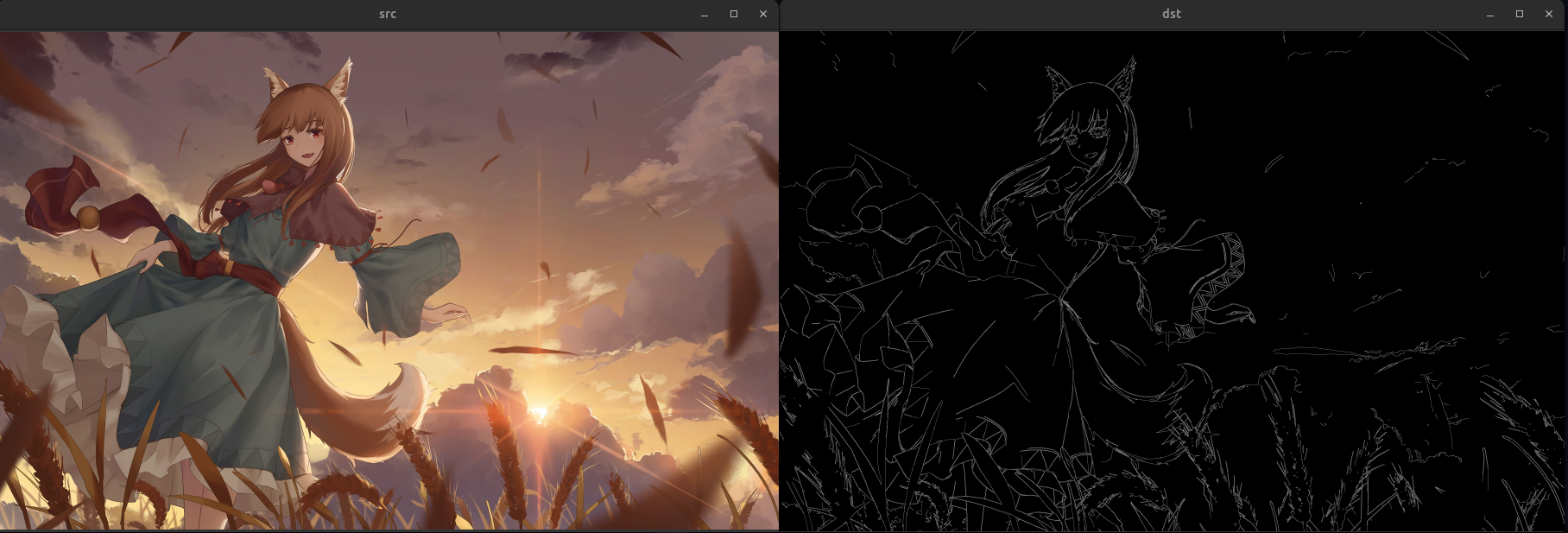
Canny 边缘检测

Canny 边缘检测是一种多步骤的边缘检测算法，它包括以下几个步骤：

高斯滤波：减少噪声
梯度计算：计算图像的梯度
非极大值抑制：抑制非边缘像素
迟滞阈值化：确定边缘

例：用 Canny 算子进行边缘检测。

#include <opencv2/opencv.hpp>

int main(int argc, char* argv[]) {
    cv::Mat src = cv::imread(argv[1]);
    cv::Mat dst;
    cv::Mat gray;

    cv::cvtColor(src, gray, cv::COLOR_BGR2GRAY); // 转换为灰度图
    cv::Canny(gray, dst, 50, 150); // Canny 边缘检测

    cv::namedWindow("src", cv::WINDOW_NORMAL);
    cv::namedWindow("dst", cv::WINDOW_NORMAL);
    cv::imshow("src", src);
    cv::imshow("dst", dst);

    cv::waitKey(0);
    return 0;
}

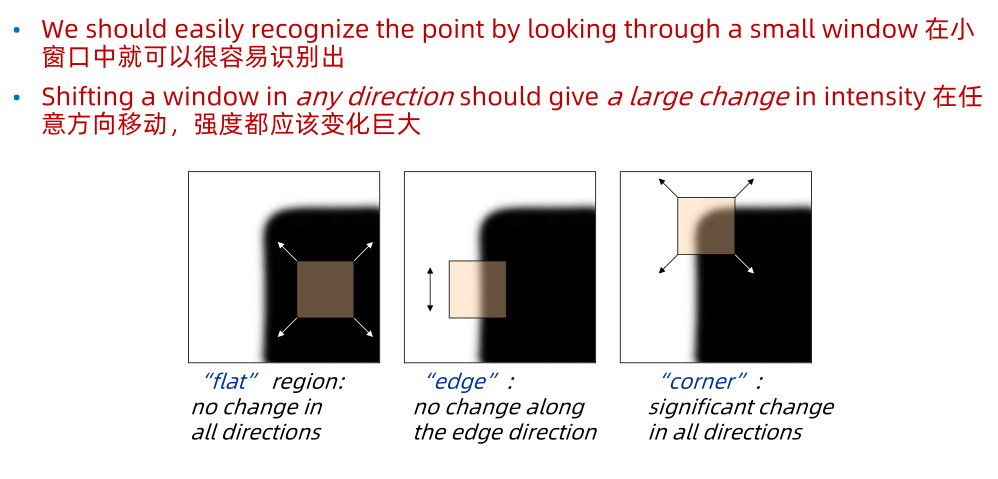
角点检测

角点是图像中的一种特殊的特征点，它是图像中的局部最大值，可以用来进行图像配准、目标跟踪等。

Harris 角点检测

Harris 角点检测是一种常用的角点检测算法，它是一种基于图像灰度的角点检测算法。

其表达矩阵可借助图像中的局部模板里两个方向梯度来定义，一种常见的表达矩阵为：

其中，是图像的梯度，是窗口函数，通常是高斯函数。

将矩阵分解为特征值和特征向量，得到两个特征值，改写为：

则角点响应函数为：

其中，是矩阵的行列式，是矩阵的迹，是一个常数。

Harris 角点检测算法的步骤如下：

计算图像的局部梯度
局部图像梯度减去均值
计算协方差矩阵
计算特征值和特征向量
利用阈值筛选角点

例：使用 Harris 角点检测算法检测角点。

#include <opencv2/opencv.hpp>

int main(int argc, char* argv[]) {
    cv::Mat src = cv::imread(argv[1]);
    cv::Mat dst;
    cv::Mat gray;
    cv::Mat dst_norm, dst_norm_scaled;

    cv::cvtColor(src, gray, cv::COLOR_BGR2GRAY); // 转换为灰度图
    cv::cornerHarris(gray, dst, 2, 3, 0.04); // Harris 角点检测
    cv::normalize(dst, dst_norm, 0, 255, cv::NORM_MINMAX, CV_32FC1, cv::Mat()); // 归一化
    cv::convertScaleAbs(dst_norm, dst_norm_scaled); // 转换为8位图

    for (int i = 0; i < dst_norm.rows; i++) {
        for (int j = 0; j < dst_norm.cols; j++) {
            if ((int)dst_norm.at<float>(i, j) > 100) {
                cv::circle(src, cv::Point(j, i), 5, cv::Scalar(0, 0, 255), 2, 8, 0);
            }
        }
    }

    cv::namedWindow("src", cv::WINDOW_NORMAL);
    cv::imshow("src", src);

    cv::waitKey(0);
    return 0;
}

形态学

主要用于图像的形状分析、特征提取等。

膨胀与腐蚀

膨胀与腐蚀是形态学中的两种基本操作，它们可以用于图像的去噪、分割等。

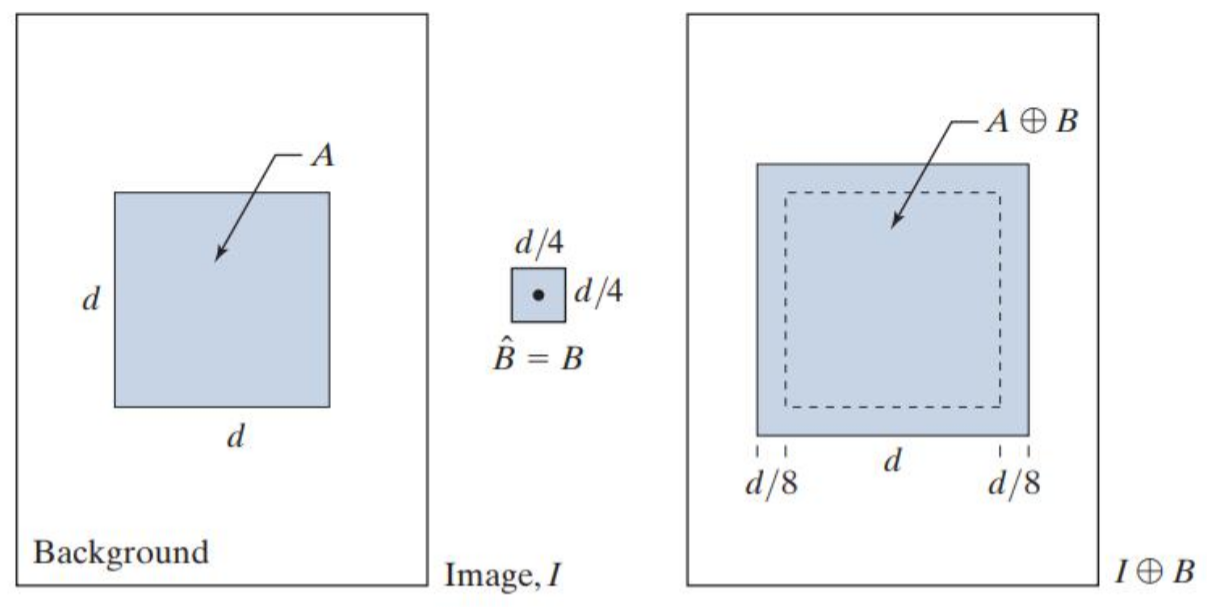
膨胀

可以使图像中的物体变大，或者连接两个物体。

其中，是原始图像，是结构元素，是膨胀操作。

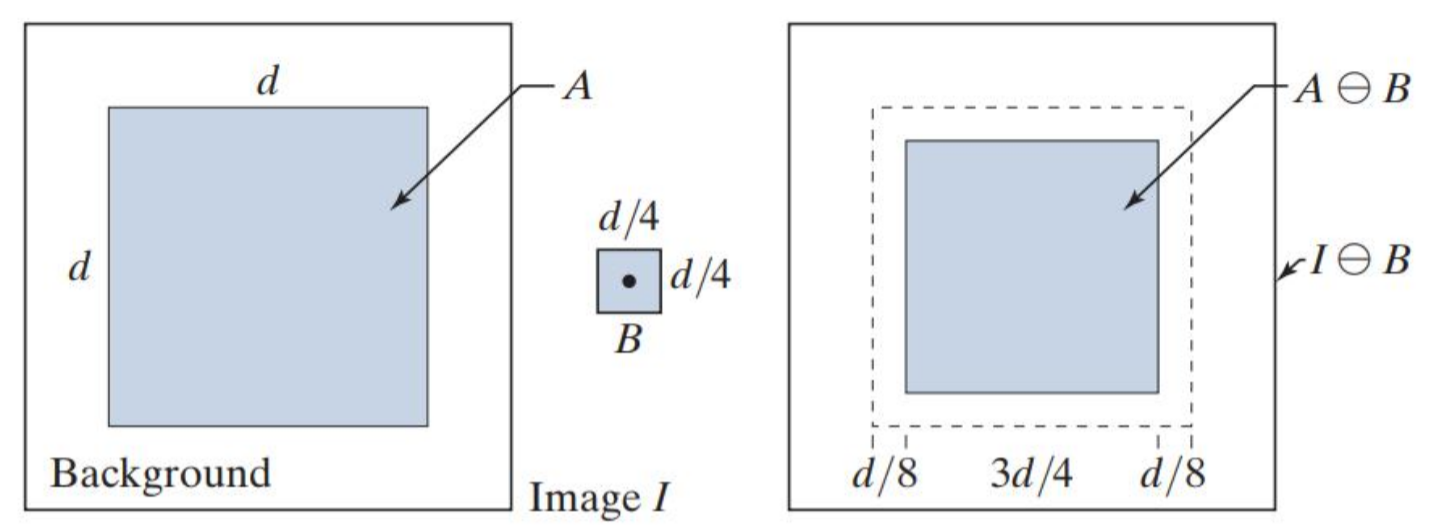
腐蚀

可以使图像中的物体变小，或者分割两个物体。

其中，是原始图像，是结构元素，是腐蚀操作。

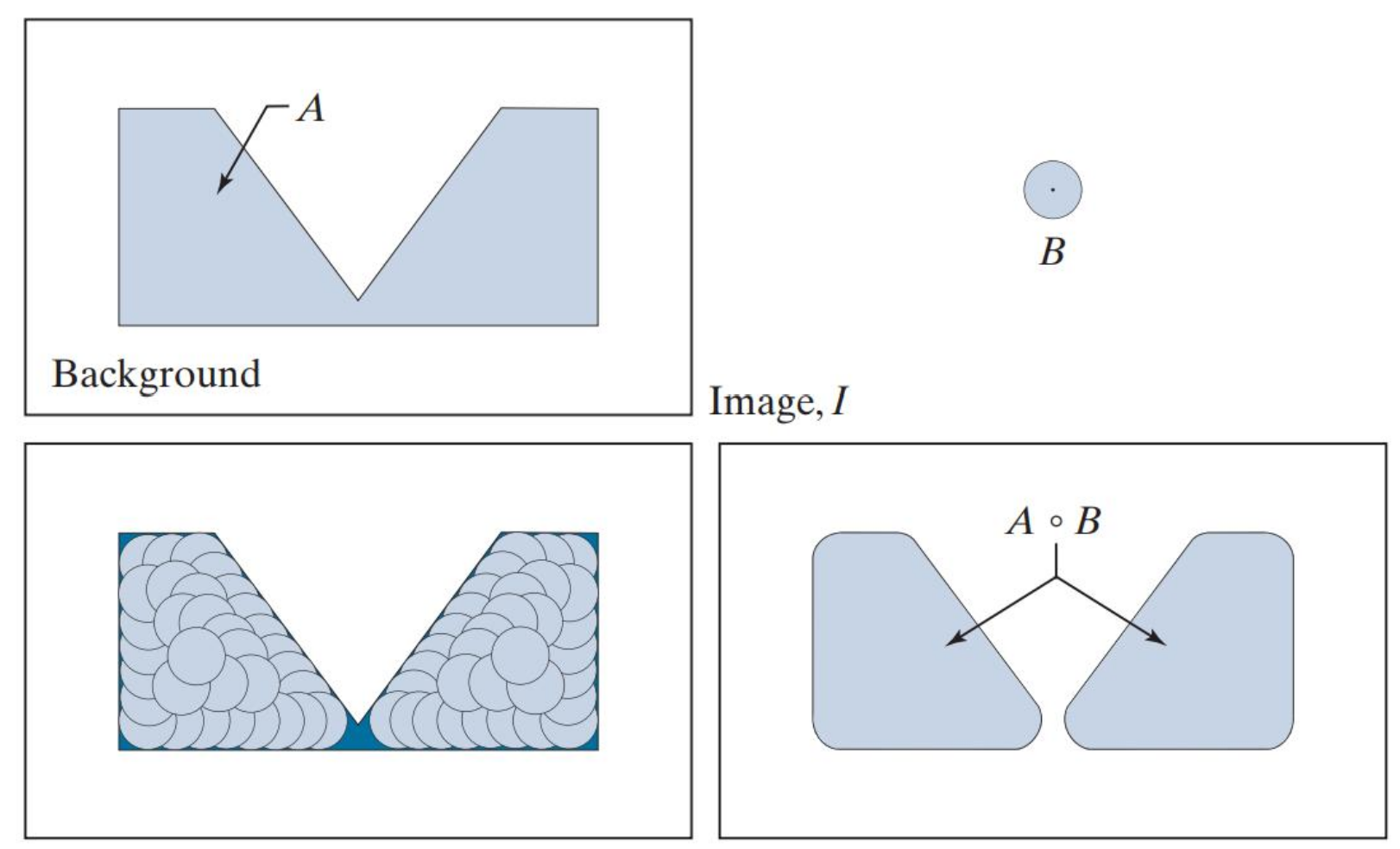
开运算与闭运算

开运算

先腐蚀后膨胀，可以去除小的噪声。

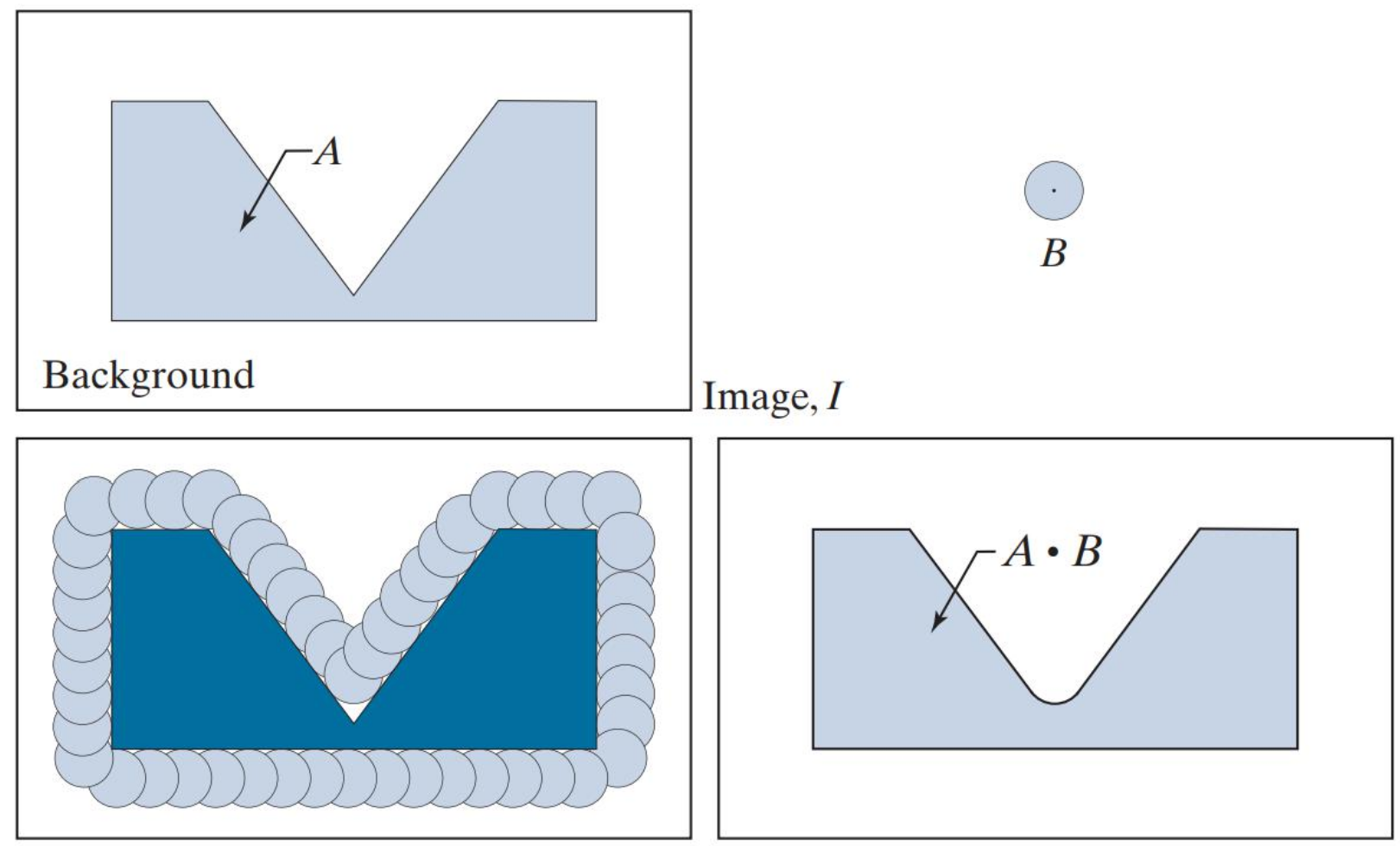
闭运算

先膨胀后腐蚀，可以填充小的空洞。

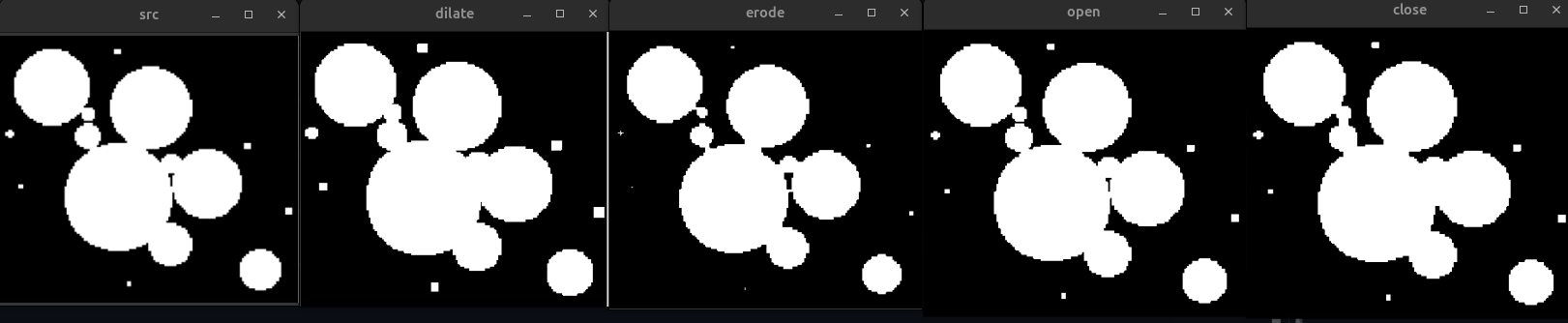
例：使用形态学操作进行图像处理。

#include <opencv2/opencv.hpp>

int main(int argc, char* argv[]) {
    cv::Mat src = cv::imread(argv[1]);
    cv::Mat dst;
    cv::Mat gray;
    cv::Mat element = cv::getStructuringElement(cv::MORPH_RECT, cv::Size(5, 5)); // 结构元素

    cv::cvtColor(src, gray, cv::COLOR_BGR2GRAY); // 转换为灰度图
    cv::threshold(gray, gray, 100, 255, cv::THRESH_BINARY); // 二值化
    
    cv::namedWindow("src", cv::WINDOW_NORMAL);
    cv::namedWindow("dilate", cv::WINDOW_NORMAL);
    cv::namedWindow("erode", cv::WINDOW_NORMAL);
    cv::namedWindow("close", cv::WINDOW_NORMAL);
    cv::namedWindow("open", cv::WINDOW_NORMAL);
    cv::imshow("src", src);
    
    cv::morphologyEx(gray, dst, cv::MORPH_DILATE, element); // 膨胀
    cv::imshow("dilate", dst);
    cv::morphologyEx(gray, dst, cv::MORPH_ERODE, element); // 腐蚀
    cv::imshow("erode", dst);
    cv::morphologyEx(gray, dst, cv::MORPH_CLOSE, element); // 闭运算
    cv::imshow("close", dst);
    cv::morphologyEx(gray, dst, cv::MORPH_OPEN, element); // 开运算
    cv::imshow("open", dst);


    cv::waitKey(0);
    return 0;
}

null-qwerty's blog